A Case for Low Bitwidth Floating Point Arithmetic on FPGA for Transformer Based DNN Inference

Abstract

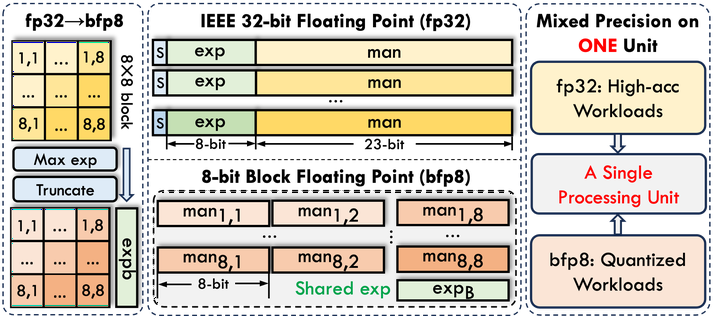
Modern Transformer-based deep neural networks are increasingly reliance on an accelerator’s ability to perform the model’s non-linear operations accurately and efficiently. Unfortunately, while conventional low bitwidth fixed-point arithmetic are superior in terms of power, performance, and area consumption for low-precision linear operations, they are not well-suited to perform non-linear operations that require large dynamic range and high precision. In this work, we present a case for using a mix of low-bitwidth block floating-point and single precision floating-point operations to address the needs of both the linear and non-linear layers of Transformer-based DNNs. To support both datatypes in hardware, an 8-bit block floating point (bfp8) processing array that can be reconfigured to implement 32-bit floating point (fp32) computation during run time is proposed. With the support of both datatypes, pre-trained Transformer models in fp32 can now be deployed without the need for quantization-aware retraining. The proposed bfp8 systolic array has been implemented efficiently on an AMD Alveo U280 FPGA, consuming only marginally more hardware resources than an int8 equivalence. It attains 2.052 TOPS throughput for the linear operations in bfp8 mode, which is equivalent to over 95% of the theoretical maximum 8-bit throughput of the target platform, while it achieves 33.88 GFLOPS throughput when operating in fp32 mode. By demonstrating the hardware efficiency of low-precision floating-point operations on FPGAs, this work provides an attractive tradeoff direction in the vast design space of accuracy, speed, power, and time-to-market for full-stack Transformer models acceleration.

Jiajun Wu

PhD Student

My research interests include Hardware accelerator, reconfigurable computing and computer architecture.